チルノのパーフェクトさんすう教室

こんにちは、ネッチ・ジャパンの篠田です。本日は、表題にありますように、さんすう、の話、もちろん熱測定に関する話です。このブログを読んでいる皆様は、99％ググっていることでしょう（笑）オタク動画が落ちています。
 
前回のブログで、私はセルポ星人ですから、とかなり謙遜して書いたのですが、そのあと社員から、確かにセルポ星人に似てますね、といわれてショックを受けたので、今回は少しまじめな話題です。
以前より、会社ではラボを中心に勉強会を開いておりますが、最近は熱物性の数学的基礎を学びなおそう、というのをやっております。テキストは、伝熱工学の進展と、JJAP 50(2011) 11RA01です。この二つを理解しておくと、単一パルス加熱に対する一次元の温度応答は、ほとんどカバーできると言えます。しかも一番解りやすい！これが重要です。繰り返しパルス加熱に対する解析解を求める方法は、馬場貴弘さんと馬場哲也先生が近年考案されたのですが、それは別途解説させて頂くとして、今回のテーマはさんすう教室ですので、基礎の基礎、一次元の熱拡散方程式のグリーン関数の導出からです。
一次元の熱拡散方程式は、
 

 
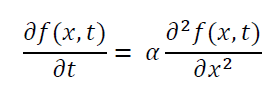
と表せます。
伝熱工学の進展の進展では、半無限物質の表面が瞬間的に加熱された時の温度応答を表すグリーン関数、

 
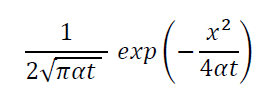
がいきなり与えられていますが、社内勉強会では当然、導出の過程まで説明が必要です。実際の有限の厚みの物体の裏面の温度応答は、仮想熱源を配置していくことによって、簡単に求めることができます。まさしくただの足し算です。
 
ちなみに、最初にかかっているは、1/√tであることに注目です。つまりかなりゆっくりと時間に対して減衰することが解ります。
これを拡張して、2次元のグリーン関数を求めると、最初にかかるのは1/tになります。
1次元のグリーン関数ですが、これはパルス加熱（デルタ関数）に対する応答ですが、実際のLFAのパルスは短いといっても有限のパルス幅があります。これを考慮にいれるには、有限のパルス幅のパルス形状をモニターして、実空間で瞬時パルスごとの応答を時間をずらして足し合わせるのも一つの手ですが（弊社の解析ソフトがこれです）、実空間の畳み込みはラプラス空間では、かけざんとなりますので、これを使って解析するうまい方法があります。
 
グリーン関数というと、ブルース・リー氏がよく実演された、ワンインチパンチを思い出します。ワンインチパンチを受けてのけぞるのがグリーン関数。ワンインチパンチの連続攻撃で、ひでぶ、となるのが実際の応答となります。（例えが古すぎて通じないのは、織り込み済みです）もちろん、線形応答システムであるのが前提です。
 
上記のJJAPの論文に書かれております。四端子行列を使うと、多層解析もパーフェクトに記述できます。これもコンセプトは非常に解りやすく、1層目の温度T1,流入する熱流q1、裏面の温度T2、熱流q2とすると、(T2,q2)と（T1,q1）の関係は、4×4の行列Aで表されます。
同様に、2層目の温度T2,流入する熱流q2、裏面の温度T3、熱流q3とすると、(T3,q3)と（T2,q2）の関係は、4×4の行列Bで表されます。つまり、2層材料の裏面(T3,q3)と加熱した表面（T1,q１）の関係は行列の積BAで表されます。かけざんです。
 
ここまでは、1次元の熱拡散の話ですが、2次元、面内の熱拡散の方程式も、足し算、掛け算でいけてしまいます。新しいアプローチをICT2025発表のネタにしておりますので、ここではちょっと。LFA467 を日本で魔改造して得られた面白いデータをお見せできると思います。
熱物性の解析には四則演算（に持ち込む）が大切、という話でした。社員にも、きっとセルボ社長でも、加減乗除くらいはできることが伝わったと願いたい今日このごろです。